Distance to the origin in multivariate normal distributions
A dimension-related analysis
I’ve been reading the Statistical Rethinking book by Richard McElreath. At some point, it mentions that in a centered multivariate normal distribution with high dimension, most of the points are far away from the origin. That is, the distance to the origin distribution is centered far away from the origin, and the higher the dimension the more far away from the origin we are.
This has a brutal consequence, which is that, if you sample from a multivariate normal distribution with high dimension, you are very unlikely to get points that are very close to the mean (and mode) of the distribution.
Let’s do an experiment to check it. First we load the libraries that we are going to need:
library(MASS)
library(purrr)
library(ggplot2)
library(dplyr)
theme_set(theme_minimal())
Now we define a function that simulates n_samples points in a
multivariate gaussian distribution with dimension dimension.
simulate_norm <- function(dimension, n_samples) {
# Sample multivariate normal distribution
# with mean in the origin
# and identity matrix standard deviation
sim_data <- mvrnorm(n = n_samples,
mu = rep(0, dimension),
Sigma = diag(dimension))
# Compute, for each sample, the l2 distance to the origin
l2_norm <- sqrt(rowSums(sim_data ** 2))
# Return the results organized in a data frame
data.frame(
l2_norm = l2_norm,
dimension = dimension
)
}
For several dimensions, we sample 20000 points and compute their distances to the origin:
dims_sim <- c(1, 5, 10, 25, 100, 400)
norm_simulations <- map_dfr(dims_sim, simulate_norm, n_samples = 20000)
Finally we plot, for each dimension, the distribution of the distances to the origin.
norm_simulations %>%
mutate(`Multivariate normal dimension` = as.factor(dimension)) %>%
ggplot(aes(x = l2_norm, color = `Multivariate normal dimension`, fill = `Multivariate normal dimension`)) +
geom_density(alpha = 0.3) +
geom_rug() +
xlab("Distance to origin")
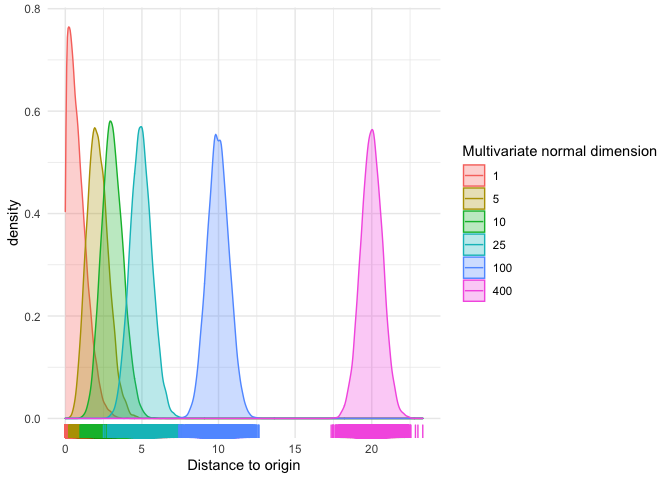
You can see that:
- The probability of being below 1 is already very low with 10 dimensions.
- For 100 dimensions, we already have very few samples with distance below 7.5.
- For a given dimension
k, the distance to the origin distribution is centered aroundsqrt(k). This is easy to prove mathematically, but not our goal.